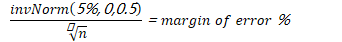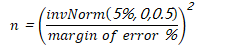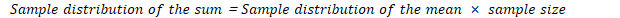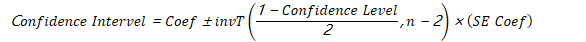Question 12
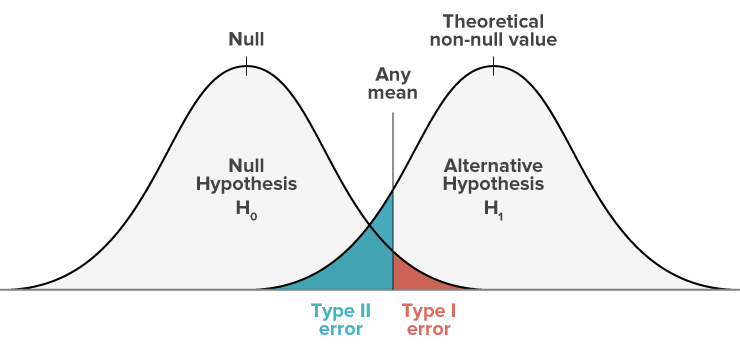
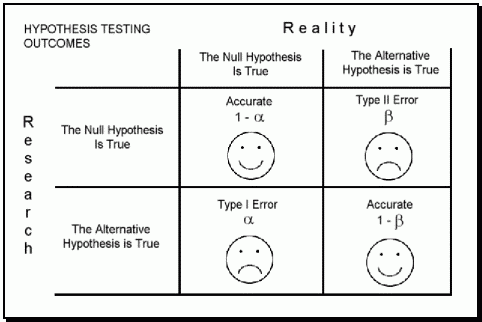

Question 15

Question 22
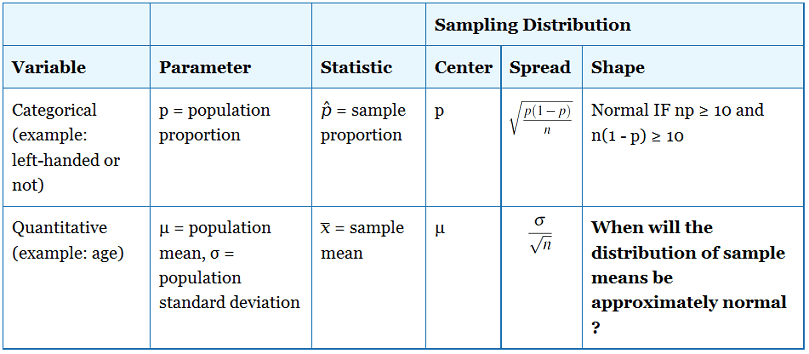
Question 23
95% confidence interval of a sampling
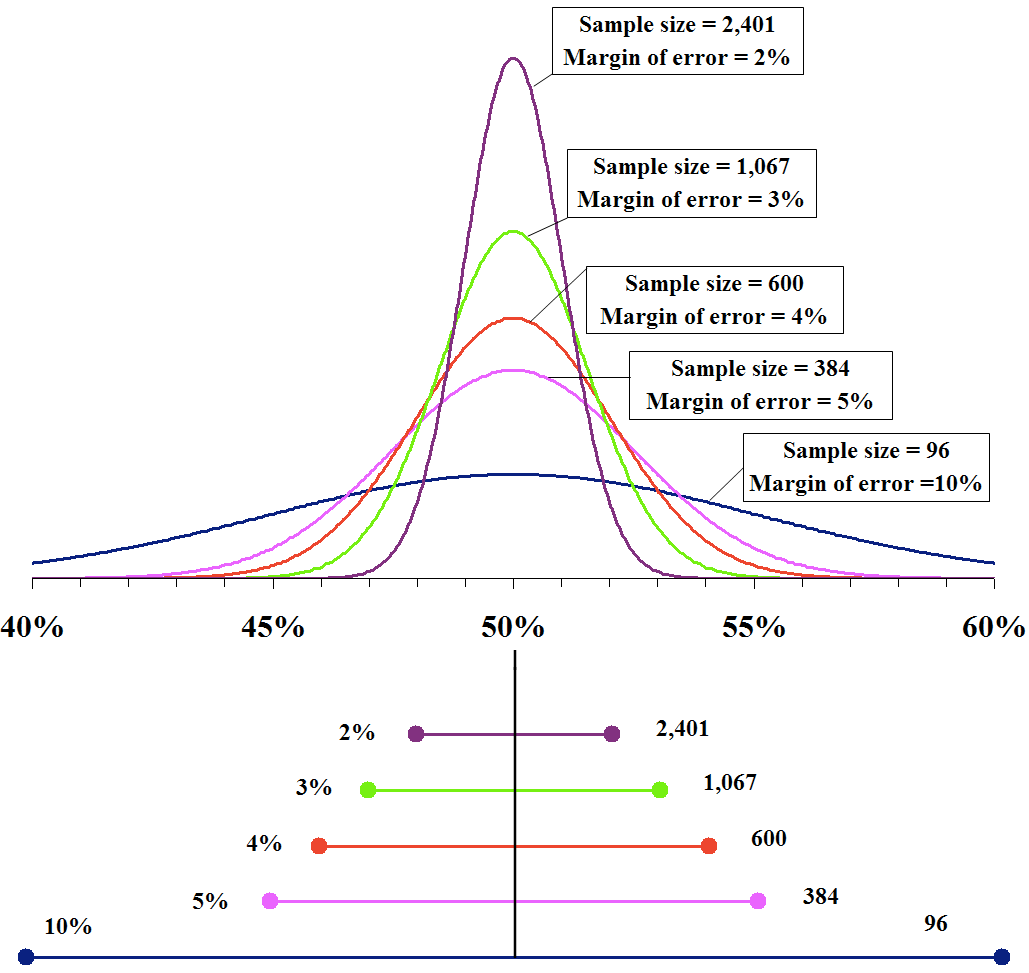
Margin of error vs. sample size at different confidence level
Equation
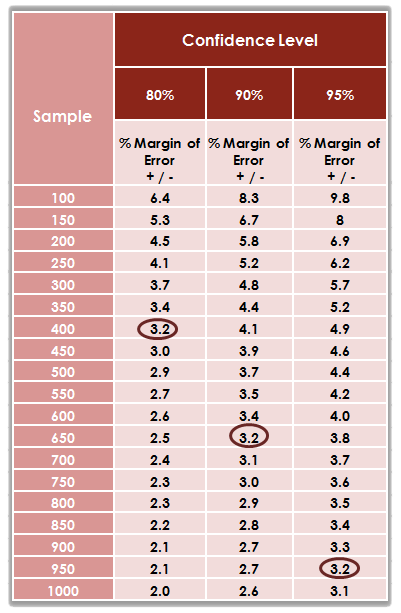
Question 25
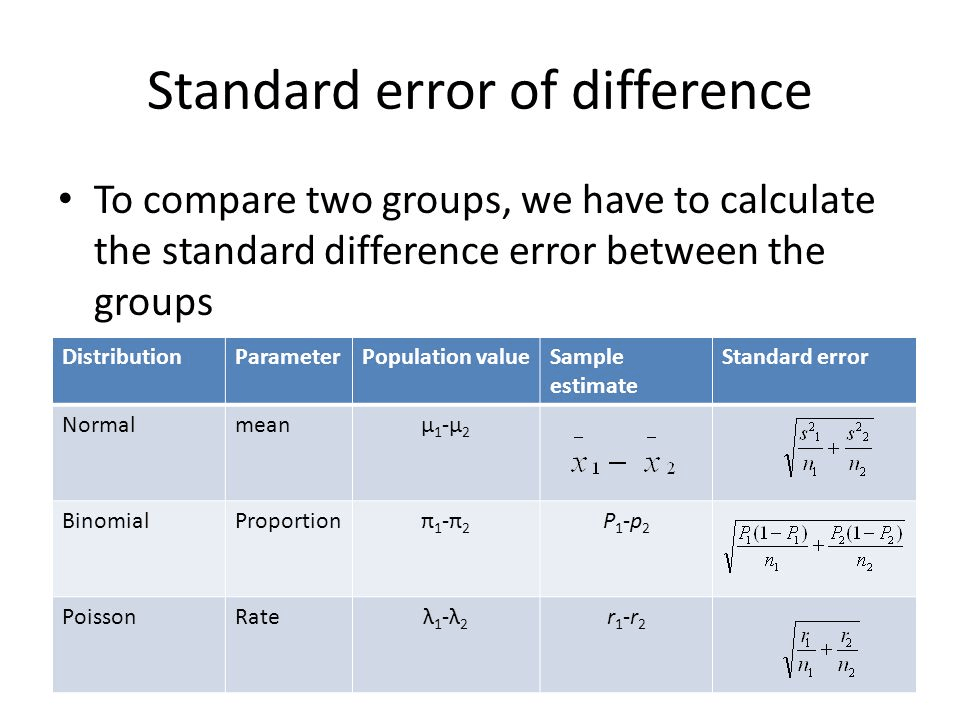
Question 26
Question 27
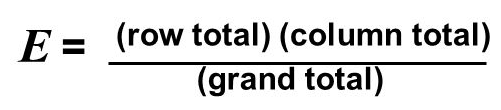

Question 30

Question 33

Question 38

Question 40
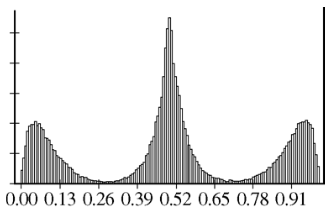
Original data
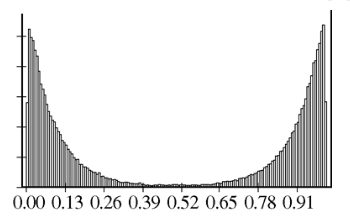
Sampling distribution of the sample mean with sample size = 2