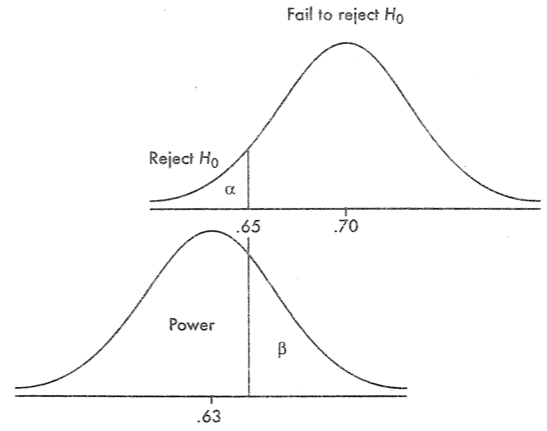
Question 16
Notice the condition
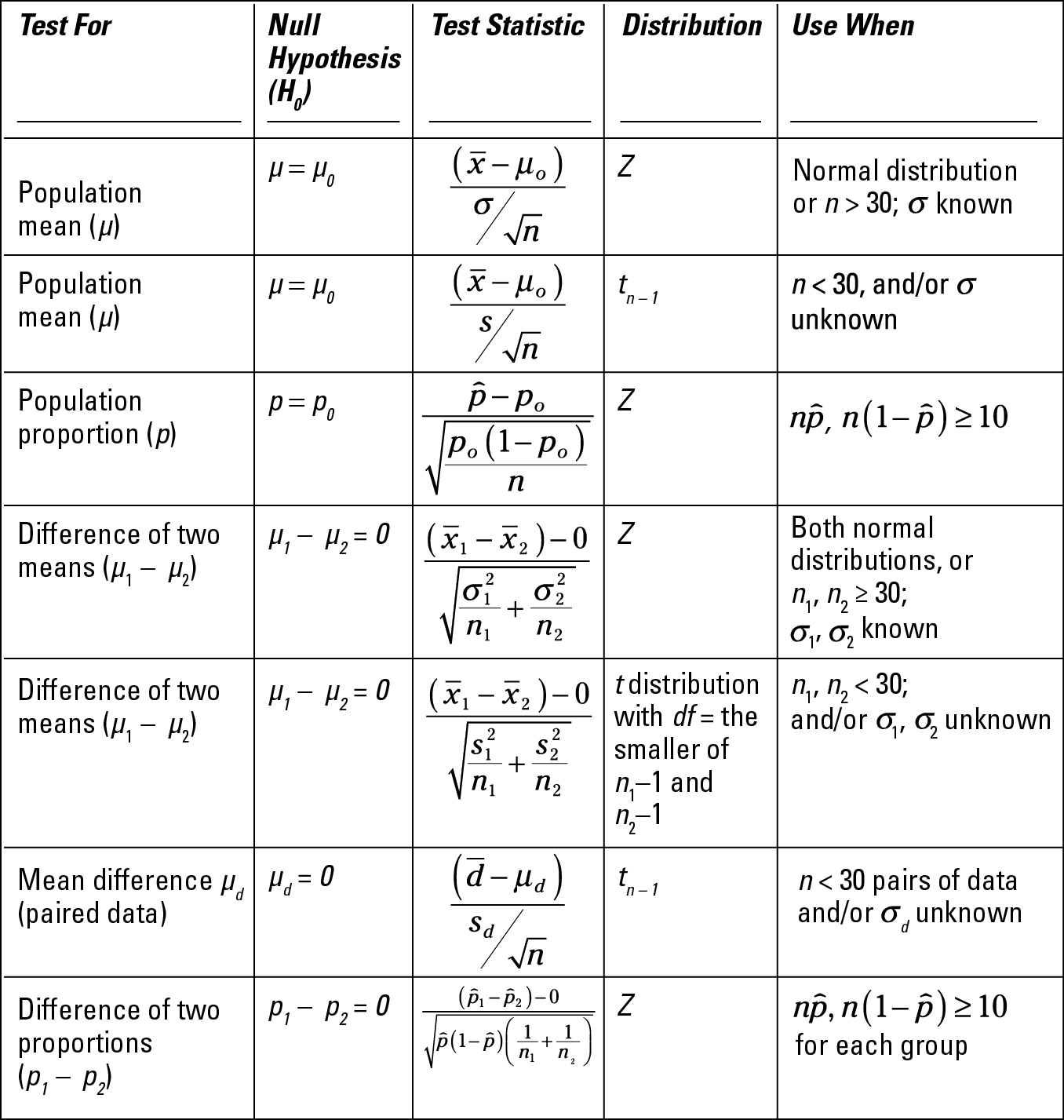
Question 18
P-value for two-sided t-test = P-value for one-sided t-test * 2

Question 21


Question 25
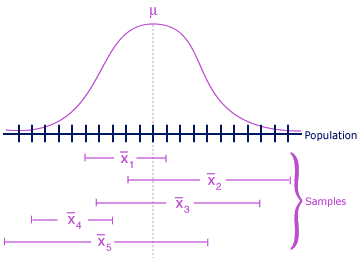
Question 31
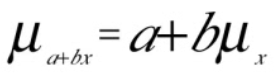
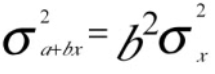
Question 32
H0: There is no association between A and B / Variables are independent
H1: There is an association between A and B / Variables are dependent
P > α
- We fail to reject the null hypothesis and do not have evidence to support the claim that there is an association between A and B
P < α
- We reject the null hypothesis and do have evidence to support the claim that there is an association between A and B
Question 37