Question 10

Question 15
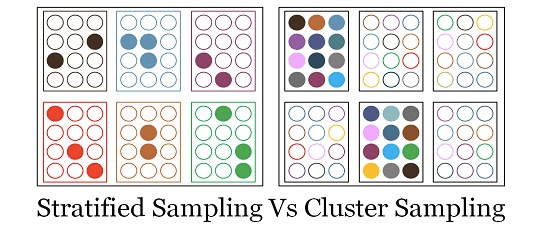
Question 16

Question 17
Residuals = observed/actual y - predicted y
See Chi-square test statistic formula
Question 18
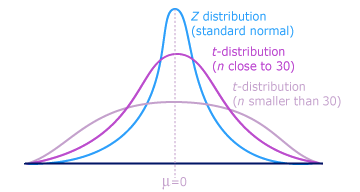
Question 19
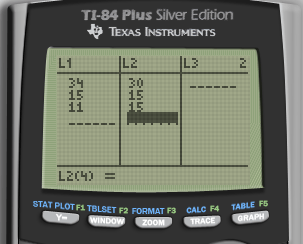
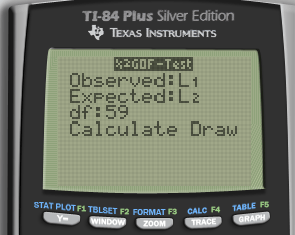
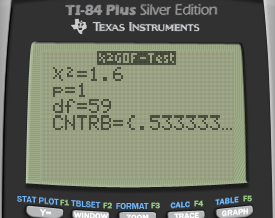
Question 23

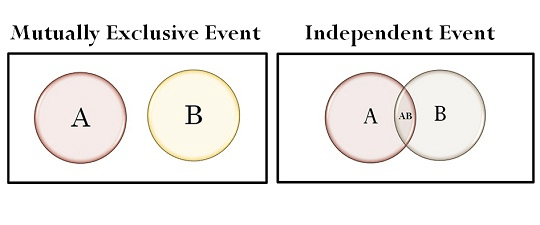
Question 24
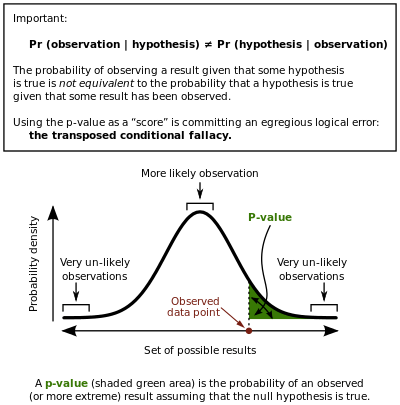
Question 34

Question 35
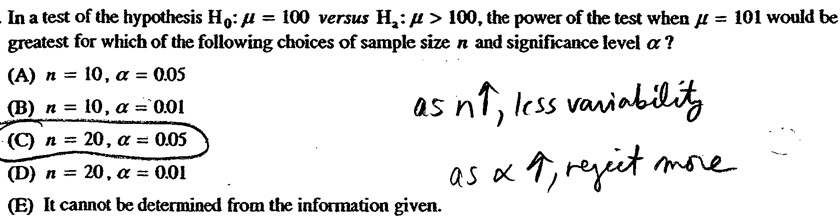
Question 37

Question 40
